本文共 2832 字,大约阅读时间需要 9 分钟。
更多深度文章,请关注:
最简单的解决方案通常是最强大的解决方案,而朴素贝叶斯就是一个很好的证明。尽管机器学习在过去几年取得了巨大的进步,但朴素贝叶斯已被证明不仅简单,而且快速、准确、可靠。它已经成功地用于许多项目中,而且它对自然语言处理(NLP)的问题的解决提供了很大的帮助。
朴素贝叶斯是利用概率论和贝叶斯定理预测样本类别(如新闻或客户评论)的概率算法。它们是概率性的,这意味着它们计算给定样本的每个类别的概率,然后输出概率最高的样本类别。他们获得这些概率的方式是使用贝叶斯定理,它基于可能与该特征相关的条件的先前数据来描述特征的概率。
我们将使用一种称为多项式朴素贝叶斯的算法。我们将以一个例子的方式介绍应用于NLP的算法,所以最终不仅你会知道这个方法是如何工作的,而且还会知道为什么它可以工作。我们将使用,使朴素贝叶斯与更复杂的机器学习算法(如SVM和神经网络)可以相提并论。
一个简单的例子
让我们看一下这个例子在实践中如何运作。假设我们正在建立一个分类器,说明文本是否涉及体育运动。我们的训练集有5句话:
| Text | Category |
| A great game(一个伟大的比赛) | Sports(体育运动) |
| The election was over(选举结束) | Not sports(不是体育运动) |
| Very clean match(没内幕的比赛) | Sports(体育运动) |
| A clean but forgettable game (一场难以忘记的比赛) | Sports(体育运动) |
| It was a close election (这是一场势均力敌的选举) | Not sports(不是体育运动) |
由于朴素贝叶斯贝叶斯是一个概率分类器,我们想要计算句子“A very close game” 是体育运动的概率以及它不是体育运动的概率。在数学上,我们想要的是P(Sports | a very close game)这个句子的类别是体育运动的概率。
但是我们如何计算这些概率呢?
特征工程
创建机器学习模型时,我们需要做的第一件事就是决定使用什么作为特征。例如,如果我们对健康进行分类,特征可能就是是一个人的身高,体重,性别等等。我们会排除对模型无用的东西,如人的名字或喜爱的颜色。
在这种情况下,我们甚至没有数字特征。我们只有文字。我们需要以某种方式将此文本转换成可以进行计算的数字。
那么我们该怎么办?一般都是使用字频。也就是说,我们忽略了词序和句子的构造,把每一个文件作为单词库来处理。我们的特征将是这些词的计数。尽管它似乎过于简单化,但它的效果令人惊讶。
贝叶斯定理
贝叶斯定理在使用条件概率(如我们在这里做)时很有用,因为它为我们提供了一种方法来扭转它们:P(A|B)=P(B|A)×P(A)/P(B)。在我们这种情况下,我们有P(sports | a very close game),所以使用这个定理我们可以逆转条件概率: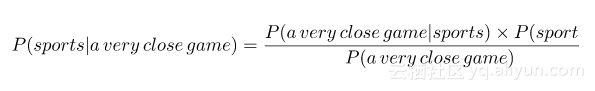
因为对于我们的分类器,我们只是试图找出哪个类别有更大的概率,我们可以舍弃除数,只是比较
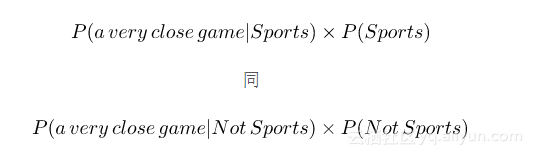
这样就更好理解了,因为我们可以实际计算这些概率!只要计算句子 “A very close game” 多少次出现在“ Sports”的训练集中,将其除以总数,就可以获得P(a very close game | Sports)。
有一个问题,但是我们的训练集中并没有出现“A very close game”,所以这个概率是零。除非我们要分类的每个句子都出现在我们的训练集中,否则模型不会很有用。
Being Naive
我们假设一个句子中的每个单词都与其他单词无关。这意味着我们不再看整个句子,而是单个单词。我们把P(A very close game)写成:P(a very close game)=P(a)×P(very)×P(close)×P(game) 这个假设非常强大,但是非常有用。这使得整个模型能够很好地处理可能被错误标签的少量数据或数据。下一步将它应用到我们以前所说的:
P(a very close game|Sports)=P(a|Sports)×P(very|Sports)×P(close|Sports)×P(game|Sports)
现在,我们所有的这些单词在我们的训练集中实际出现了好几次,我们可以计算出来!
计算概率
计算概率的过程其实只是在我们的训练集中计数的过程。
首先,我们计算每个类别的先验概率:对于训练集中的给定句子, P(体育运动)的概率为⅗。然后,P(非体育运动)是⅖。然后,在计算P(game | Sports)就是“game”有多少次出现在sports的样品,然后除以sports的总数(11)。因此,P(game|Sports)=2/11。
但是,我们遇到了一个问题:“close”不会出现在任何sports样本中!那就是说P(close | Sports)= 0。这是相当不方便的,因为我们将把它与其他概率相乘,所以我们最终会得到P(a|Sports)×P(very|Sports)×0×P(game|Sports)等于0。这样做的事情根本不会给我们任何信息,所以我们必须找到一个办法。
我们该怎么做呢?通过使用一种被称为的方法:我们为每个计数添加1,所以它不会为零。为了平衡这一点,我们将可能的词数加到除数,因此这部分将永远不会大于1。在我们的案例中,可能的话是 [ “a” ,“great” ,“very” ,“over” ,'it' ,'but' ,'game' ,'election' ,'close' ,'clean' ,'the' ,'was' ,'forgettable' ,'match' ] 。
由于可能的单词数是14,应用拉普拉斯平滑我们得到了。全部结果如下: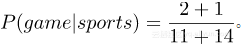
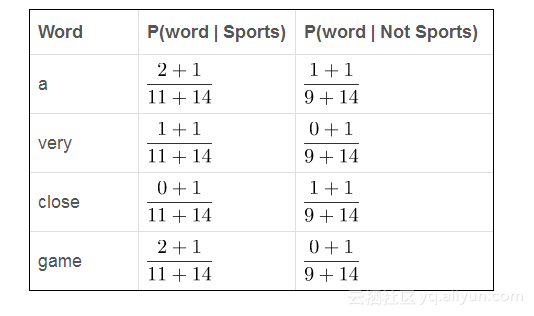
现在我们只是将所有的概率加倍,看看谁更大:

完美!我们的分类器给出了“A very close game” 是Sport类。
先进的技术
改进这个基本模型可以做很多事情。以下这些技术可以使朴素贝叶斯与更先进的方法效果相当。
- (删除停用词)。这些常用的词,不会真正地添加任何分类,例如,一个,有能力,还有其他,永远等等。所以为了我们的目的,选举结束将是选举,一个非常接近的比赛将是非常接近的比赛。
- (单词变体还原)。这是将不同的词汇组合在一起的。所以选举,大选,被选举等将被分组在一起,算作同一个词的更多出现。
- (使用实例)。我们可以计算一些常用的实例,如“没有内幕的比赛”和“势均力敌的选举”。而不只是一个字,一个字的进行计算。
- 。而不是只是计数频率,我们可以做更高级的事情
本文由北邮推荐,翻译。
文章原标题《A practical explanation of a Naive Bayes classifier》
作者:,机器学习爱好者,译者:袁虎,审阅:
文章为简译,更为详细的内容,请查看
转载地址:http://qyzoa.baihongyu.com/